Fixed-Radius Neighbour Search Using Thrust #

This page describes how one might implement the pair-finding algorithm described by Simon Green (2010). Many implementations of Simon’s work exists, such as the FRNN Python package.

Why Thrust? #

I would argue that there is a fairly strong incentive to make GPU-accelerated codes portable across different hardware platforms. At the time of writing, NVIDIA GPUs are becoming more challenging to get a hold of, and are more expensive relative to their competition (i.e., AMD and Intel GPUs). Consequently, it is becoming harder to justify writing code exclusively using the CUDA ecosystem.

While Thrust was originally exclusive to NVIDIA platforms, AMD have developed their own implementation and Intel’s OneDPL provides similar functionality with an almost identical API (see their article describing how to port Thrust applications to OneDPL).

Thrust is also high-level and aims to replicate the STL and includes many optimised algorithms such as sorting and scanning, which will be leveraged here. This means using Thrust avoids the need of having to self-write these algorithms (like what the FRNN package does), is comparatively easy to understand for existing C++ developers, and is portable.

The algorithm #

Simon’s article already does a good job of describing how the pair-search algorithm is supposed to work, so I will defer the high-level description to that paper.

However, Simon’s paper stops at creating the uniform grid using sorting, and creating an array indicating the starts of the cells. Here, I show the steps beyond.

In this algorithm, after the particle-to-grid mapping is created, we determine

The details #

Here, I’m writing the algorithm inside a function, assuming it will be called elsewhere. The function will take in three thrust::device_vector<F>, where F is a template type. It will also take a singular F value, which represents the cutoff radius which defines an interacting pair. Importantly, the input device vectors must be passed by reference, because they will be permuted based on the sorting. The function will return a std::pair of device vectors, where each device vector represents one of the sides of the output pairs found. A template parameter, I will be used to specify the integer type of the indices. Thus, the function definition will look like:

#include <thrust/host_vector.h>                // thrust::host_vector
#include <thrust/device_vector.h>              // thrust::device_vector
#include <thrust/sort.h>                       // thrust::sort_by_key
#include <thrust/gather.h>                     // thrust::gather
#include <thrust/iterator/counting_iterator.h> // thrust::counting_iterator
#include <utility>                             // std::pair
#include <thrust/remove.h>                     // thrust::remove_if
#include <thrust/sequence.h>                    // thrust::sequence
#include <nvtx3/nvToolsExt.h>                  // nvtxRangePush, nvtxRangePop

template<typename F, typename I>
std::pair<thrust::device_vector<I>, thrust::device_vector<I>> find_pairs(
        thrust::device_vector<F> &x,
        thrust::device_vector<F> &y,
        thrust::device_vector<F> &z,
        const F cutoff
    )
{
    nvtxRangePush("find_pairs");
    // body ...
    nvtxRangePop();
}

nvtx3/nvToolsExt.h is included so the NVTX ranges can be used for profiling with NSight Systems. Both the whole function smaller regions will have function calls.

Defining Algorithm Constants #

To mitigate mistakes and make the code easier to read, lets define constants related to the algorithm.

// define constants
                // cell size is cutoff/cells_per_cutoff
constexpr int cells_per_cutoff = 1,
                // the length of the cube that forms the search space (units: no. of cells)
                search_cube_len = 2*cells_per_cutoff + 1,
                // no. of adjacent cells to search
                n_search_adj_cells = (search_cube_len*search_cube_len*search_cube_len - 1)/2,
                // no. of cells to search i.e. the number of adjacent cell plus the particle's own cell.
                n_search_all_cells = n_search_adj_cells + 1;

// inside function body
// size of each cell
const F cell_size = cutoff/F(cells_per_cutoff);

In Simon’s paper, each cell in the algorithm is equal to the length of the cutoff distance. Later, we’ll explore this number. The remaining constants are derivative numbers related to this ratio.

Finding the grid extents #

The first step is to find the extents of the grid that encapsulates the particle cloud. Thrust offers the minmax_element function in the thrust/extrema.h header file, which can be used here:

    nvtxRangePush("grid extents");

    // declare the min-max extent arrays
    F mingrid[3], maxgrid[3];
    // find the extents
    auto res = thrust::minmax_element(x.begin(), x.end());
    mingrid[0] = *(res.first);
    maxgrid[0] = *(res.second);
    res = thrust::minmax_element(y.begin(), y.end());
    mingrid[1] = *(res.first);
    maxgrid[1] = *(res.second);
    res = thrust::minmax_element(z.begin(), z.end());
    mingrid[2] = *(res.first);
    maxgrid[2] = *(res.second);

    // extend the grid to ensure there are buffer cells
    for (int d = 0; d < 3; ++d) {
        mingrid[d] -= F(2.)*cutoff;
        maxgrid[d] += F(2.)*cutoff;
    }

Important to note here that the return type of thrust::minmax_element is a pair of device_ptr which must be dereferenced to be stored in the mingrid, maxgrid arrays. minmax_element is called three times - one for each coordinate. Finally, the minima and maxima of the grid are extended so that when adjacent cells of particles are searched later, they stay within the bounds.

Before continuing to the next step, we can calculate the number of cells in each direction:

    const int ngrid[3] {
        static_cast<int>((maxgrid[0]-mingrid[0])/cell_size) + 1,
        static_cast<int>((maxgrid[1]-mingrid[1])/cell_size) + 1,
        static_cast<int>((maxgrid[2]-mingrid[2])/cell_size) + 1
    };

    nvtxRangePop();

Which rounds up the number of grid cells. Optionally, you can update the maxima of the grid, but isn’t really necessary as the maxima aren’t used from herein. The “grid extents” NVTX region is also stopped.

Mapping the particles to the grid and sorting #

This is the step that Simon’s paper illustrates. First we must determine the grid cell indices that each cell belongs to. As per Simon’s paper, we’re using a scalar “hash” to map particles to grid cells. This 1D hash is beneficial for two reasons:

the algorithm itself is sped up as less data is transferred when retrieving the grid indices
spatial locality is improved.

First assigning particles to grid cells:

    nvtxRangePush("map points to grid");

    // declare array to store particles' grid indices
    thrust::device_vector<int> gidx(x.size());
    // this makes the device vector's data accessible in the lambda
    const thrust::device_ptr<int> d_gidx {gidx.data()};

    // map particles to grid
    thrust::transform(
        thrust::make_zip_iterator(thrust::make_tuple(x.begin(), y.begin(), z.begin())),
        thrust::make_zip_iterator(thrust::make_tuple(x.end(), y.end(), z.end())),
        gidx.begin(),
        [=] __device__ (const thrust::detail::tuple_of_iterator_references<F&, F&, F&> in) {
            const int idxx = static_cast<int>((thrust::get<0>(in)-mingrid[0])/cell_size), // x grid index
                      idxy = static_cast<int>((thrust::get<1>(in)-mingrid[1])/cell_size), // y grid index
                      idxz = static_cast<int>((thrust::get<2>(in)-mingrid[2])/cell_size); // z grid index
            return idxy*ngrid[1]*ngrid[2] + idxx*ngrid[2] + idxz; // convert to 1D grid index and return
        }
    );
    
    nvtxRangePop();

There’s a lot going on here so let’s break it down:

thrust::transform
- is used to transform the values of an input iterator, and place them in an output iterator (in this case, gidx).
thrust::make_zip_iterator(thrust::make_tuple(...))
- this “packs” the forward iterators as provided by x/y/z.begin(), so that each thrust::transform iteration has access to the corresponding x, y, and z values.
gidx.begin()
- specifies that the output is to be placed in gidx.
[=] __device__ (...)
- is a lambda (can be used since compute capability 7.0). [=] specifies that external values should be captured by value. Capturing external variables by reference is unavailable in a CUDA lambda. The __device__ attribute specifes that the generated lambda instructions is for the device aka GPU.
- the lambda accepts a thrust::detail::tuple_of_iterator_references, which is a tuple of each of the x, y, z values. These values, are retrieved with the thrust::get<i> function, where i is an index.
- static_cast<I>((thrust::get<i>(in) - mingrid[i])/cutoff) is obtaining the grid index in the ith direction. The “hashing” function ensures that that the grid is “column major” i.e., the third index is consecutive in memory.

Now that each particle has been assigned a grid cell index, we can sort the grid cells, and obtain a mapping of old array indices to new ones.

    nvtxRangePush("sort particles");

    // sort particles based on grid index. Performed in a block to manage scratch space.
    {
        // initialize permute
        thrust::device_vector<int> permute(x.size());
        thrust::sequence(permute.begin(), permute.end()); // e.g., 0 1 2 3 4

        // sort gidx
        thrust::sort_by_key(thrust::device, gidx.begin(), gidx.end(), permute.begin());
        /* e.g. before gidx = 1 9 2 8 3, permute = 0 1 2 3 4
                after  gidx = 1 2 3 8 9, permute = 0 2 4 3 1 */

        // gather old positions into new ones
        thrust::device_vector<F> tmp(x.size());
        thrust::gather(thrust::device, permute.begin(), permute.end(), x.begin(), tmp.begin());
        /* e.g. before x = 0.1 0.5 0.1 0.5 0.3, tmp = ?   ?   ?   ?   ?
                after  x = "                 ", tmp = 0.1 0.1 0.3 0.5 0.5 */
        thrust::copy(thrust::device, tmp.begin(), tmp.end(), x.begin());
        // e.g.        x = 0.1 0.1 0.3 0.5 0.5
        // repeat for y, z
        thrust::gather(thrust::device, permute.begin(), permute.end(), y.begin(), tmp.begin());
        thrust::copy(thrust::device, tmp.begin(), tmp.end(), y.begin());
        thrust::gather(thrust::device, permute.begin(), permute.end(), z.begin(), tmp.begin());
        thrust::copy(thrust::device, tmp.begin(), tmp.end(), z.begin());
    }

    nvtxRangePop();

Hopefully the examples in the comments are enough to illustrate what’s going on. But, at a high-level, the permute vector is initialized with numbers 0 to the length of permute (which is the same as gidx). Then, thrust::sort_by_key sorts the gidx vector, as well as updating permute such that the ith element of permute corresponds to the old position of the ith element in the now sorted gidx vector. thrust::gather is then used to permute the old x/y/z vectors into their new positions in a temporary vector, which is then copied back to the original vector using thrust::copy. Unfortunately, there’s no way that I know of to do this in a single function.

Finding the cell end indices #

In Simon’s paper, the start of each cell in gidx is obtained. But here, the end of each cell is obtained. The ends are recorded instead of the starts as the algorithms are a little more convenient to write.

    nvtxRangePush("find cell ends");

    // initialize cell_ends vector and initialize to 0
    thrust::device_vector<int> cell_ends(ngrid[0]*ngrid[1]*ngrid[2], 0);
    // create device_ptr needed for lambda
    thrust::device_ptr<int> d_cell_ends {cell_ends.data()};
    thrust::for_each(
        thrust::counting_iterator<int>(1), 
        thrust::counting_iterator<int>(gidx.size()), 
        [=] __device__ (const int i) {
            const int this_cell = d_gidx[i], prev_cell = d_gidx[i-1];
            if (this_cell != prev_cell) d_cell_ends[prev_cell] = i;
        }
    );
    // e.g. gidx = 1 2 3 8 9, cell_ends = 0 1 2 3 0 0 0 0 0 4 5 0
    thrust::inclusive_scan(thrust::device, cell_ends.begin(), cell_ends.end(), cell_ends.begin(), thrust::maximum<int>());
    // e.g. cell_ends = 0 1 2 3 3 3 3 3 3 4 5 5

    nvtxRangePop();

After the initialization of the cell_ends vector (which is hopefully self-explanatory), two device pointers are generated, pointing to the underlying data of cell_ends and gidx.

The thrust::for_each function is effectively a for loop and serves a similar purpose to std::for_each. thrust::counting_iterator is used to specify that range of the loop. A lambda is used to define the work done in each iteration of the loop, which is to first check whether the ith entry of gidx is different from the previous entry. If it is different, that means the ith element is recorded as the end of the cell gidx[i-1], so cell_ends is updated. Note:

lambdas cannot use the device_vector accessor operator ([]), hence the need to create a device_ptr.
after the for_each, cell_ends possesses zeroes in cell indices which aren’t in gidx.

cell_ends can be used even with zeroes, but it’s more convenient to ensure that they are filled with something meaningful. Here, the intention is to use cell_ends to specify the range of particle indices that belong to a cell. For example, if cell_ends = 0 1 2 3 0 0 0 0 0 4 5 0, then the start of cell 3 is found at cell_ends[2], and the end is found at cell_ends[3] (open-interval). If the zeroes remain, then for cell 8, the the start may be specified as cell_ends[7] = 0, and the end is cell_ends[8] = 4, which is not correct. If the zeroes are “filled” with a sensible value, then we can use cell_ends[i-1] as the first particle index for cell i.

Hence, thrust::inclusive_scan, with a thrust:maximum binary functor fills in the zeroes with the largest value up to that index. In the previous example, you should be able to see that cell_ends[7] = 3, providing the correct starting particle index to use for cell 8.

Generating potential pairs #

In my version of the finding pair algorithm, I avoid using atomics as they can degrade performance significantly in cases where there is high-contention (i.e., many threads are trying to update the same variable). In addition, AMD GPUs don’t do atomic operations that well. To avoid atomics, I generate potential pairs first, and then compacting these pairs into realised pairs.

When generating potential pairs, it’s important to understand that for each particle, only half the neighbouring cells need to be searched. This is because finding pairs is symmetric i.e., if one particle is found to be paired with another, I don’t need to do the reverse check. Consequently, for each particle, only the “lowest” 14 cells are searched for neighbours (one of those cells being its own). See the figure below for an illustration and note that cell indices are relative to the particle of interest’s cell.

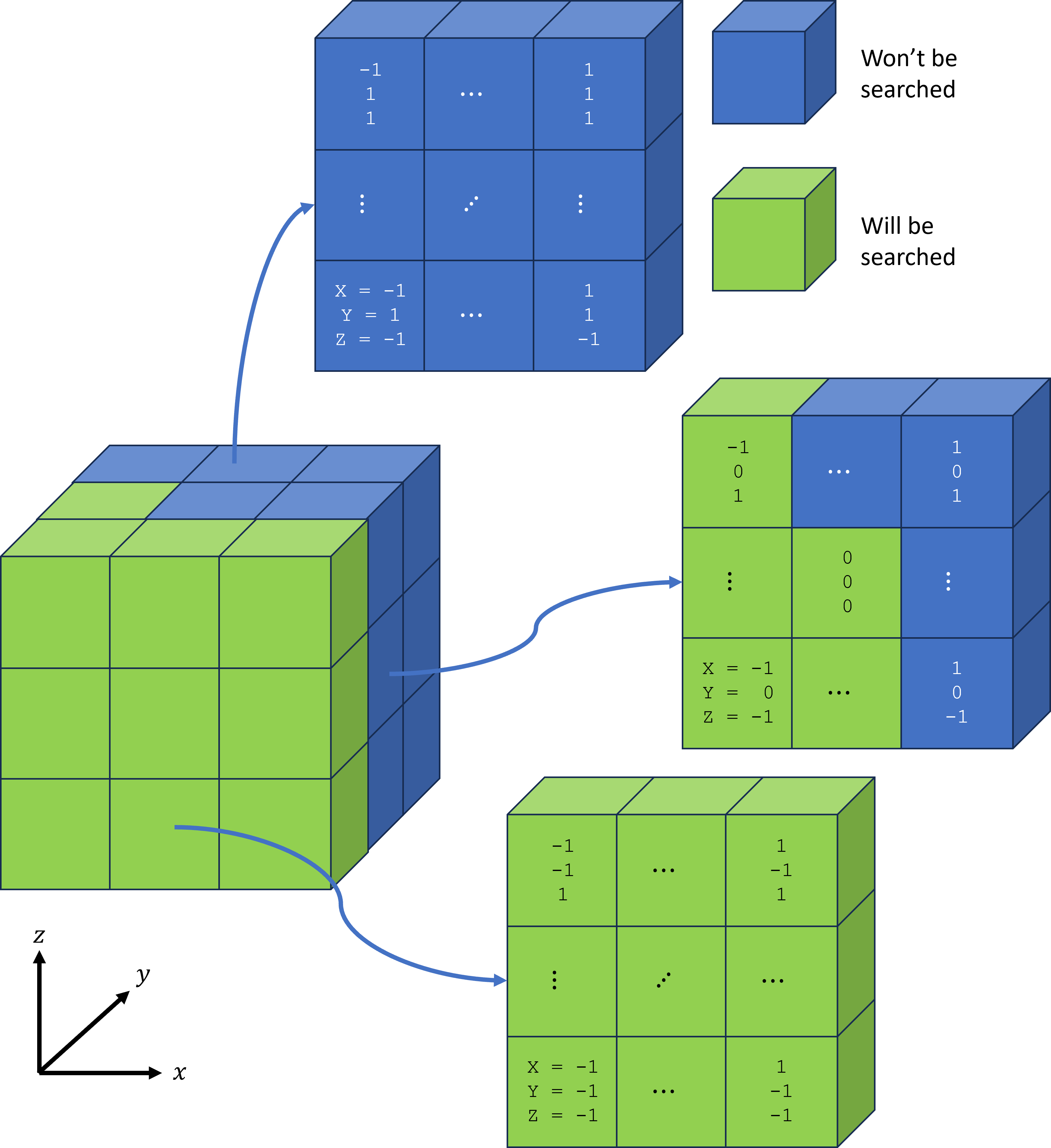
Given that each particle will check a cell for neighbours, we must first figure out how many checks will be done.

    nvtxRangePush("populate nchecks");

    // initialize number of checks
    thrust::device_vector<size_t> nchecks(n_search_all_cells*x.size());
    thrust::device_ptr<size_t> d_nchecks {nchecks.data()};

    // populate nchecks
    thrust::for_each(
        thrust::counting_iterator<int>(0),
        thrust::counting_iterator<int>(x.size()),
        [=] __device__ (const int i) {
            const int loc = n_search_all_cells*i, my_idx = d_gidx[i];
            int start_idx = my_idx - cells_per_cutoff*ngrid[2]*ngrid[1] - cells_per_cutoff*ngrid[2] - cells_per_cutoff;
            for (int j = 0; j < n_search_all_cells; ++j) {
                // which cell am i comparing to?
                const int idxz = j % search_cube_len,
                          rem = j / search_cube_len, 
                          idxy = rem % search_cube_len, 
                          idxx = rem / search_cube_len;
                const int neighbour_idx = start_idx + idxx*ngrid[1]*ngrid[2] + idxy*ngrid[2] + idxz;
                // get the starting particle index
                const int start_pidx = d_cell_ends[neighbour_idx-1];
                const int end_pidx = j==n_search_adj_cells ? i : d_cell_ends[neighbour_idx];
                d_nchecks[loc+j] = static_cast<size_t>(end_pidx - start_pidx);
            }
        }
    );

After nchecks is initialized, a thrust::for_each call is used, using the thrust::counting_iterator to specify the iteration range. As many threads as there are particles is launched, where each thread is responsible for generating the number checks to be done for the relevant neighbouring cells.

Now, we can get the total number of checks to be performed:

    const size_t last_ncheck_prescan = nchecks.back();
    thrust::exclusive_scan(thrust::device, nchecks.begin(), nchecks.end(), nchecks.begin());
    const size_t nchecks_total = last_ncheck_prescan + nchecks.back();

    nvtxRangePop();

The thrust::exclusive_scan turns the nchecks vector into a vector that specifies the starting index within the potential pair list that correspond to a particle i and one of its neighbouring cells. With that information, the actual generation of potential pairs can be performed.

    nvtxRangePush("generate potential pairs");

    // initialize potential pair list
    thrust::device_vector<int> potential_pairs_i(nchecks_total), potential_pairs_j(nchecks_total);
    thrust::device_ptr<int> d_potential_pairs_i(potential_pairs_i.data()), d_potential_pairs_j(potential_pairs_j.data());

    // allocate vector to flag which potential pair is an actual pair
    thrust::device_vector<bool> is_neighbour(nchecks_total);
    const thrust::device_ptr<bool> d_is_neighbour {is_neighbour.data()};

    // search potential pairs and flag actual pairs
    thrust::for_each(
        thrust::counting_iterator<int>(0),
        thrust::counting_iterator<int>(nchecks.size()),
        [=] __device__ (const int ii) {
            const int i = ii/n_search_all_cells, neighbour = ii % n_search_all_cells;
            const int my_idx = d_gidx[i], 
                      start_idxz = neighbour % search_cube_len, 
                      rem = neighbour/search_cube_len, 
                      start_idxx = rem / search_cube_len, 
                      start_idxy = rem % search_cube_len;
            const int neighbour_idx = 
                      my_idx + 
                      ngrid[1]*ngrid[2]*(start_idxx-cells_per_cutoff) + 
                      ngrid[2]*(start_idxy-cells_per_cutoff) + 
                      (start_idxz - cells_per_cutoff);
            const int start_idx = d_cell_ends[neighbour_idx - 1], 
                      end_idx = neighbour==n_search_adj_cells ? i : d_cell_ends[neighbour_idx];
            size_t loc = d_nchecks[ii];
            const F xi = d_x[i], yi = d_y[i], zi = d_z[i];
            for (int j = start_idx; j < end_idx; ++j) {
                const F dx = xi - d_x[j], dy = yi - d_y[j], dz = zi - d_z[j];
                d_is_neighbour[loc] = (dx*dx + dy*dy + dz*dz < cutoff*cutoff);
                // faster to always save pairs - even if not an actual pair.
                d_potential_pairs_i[loc] = i;
                d_potential_pairs_j[loc] = j;
                loc++;
            }
        }
    );

    nvtxRangePop();

This step is quite complex, but hopefully the comments are sufficient. The potential pair list can be compacted with a remove_if:

    nvtxRangePush("compact potential pairs");

    potential_pairs_i.erase(
        thrust::remove_if(
            potential_pairs_i.begin(), 
            potential_pairs_i.end(), 
            is_neighbour.begin(), 
            thrust::logical_not<bool>()
        ),
	    potential_pairs_i.end()
    );
    potential_pairs_j.erase(
        thrust::remove_if(
            potential_pairs_j.begin(), 
            potential_pairs_j.end(), 
            is_neighbour.begin(), 
            thrust::logical_not<bool>()
        ),
	    potential_pairs_j.end()
    );

    nvtxRangePop();

    // return indices as a pair of vectors
    std::pair<thrust::device_vector<int>, thrust::device_vector<int>> 
        pairs_out(
            std::move(potential_pairs_i), 
            std::move(potential_pairs_j)
        );

    // end of the range started at the start of the function
    nvtxRangePop();

    return pairs_out;

Results #

To test the performance we use the following test case:

1,000,000 particles
positions generated randomly such that each coordinate is between 0 and 1
positions stored as double precision (relevant in simulation codes)
positions already sent to GPU.
cutoff radius is 0.03 (3 times the average particle spacing).
run on an A100 PCIE
compiled with nvcc -O3 --use_fast_math --extended-lambda --compiler-options "-march=native -mtune=native" using CUDA 12.2 with gcc 11.2.0 used as the base.
- Latest CUDA at time of writing is 13.0 and latest gcc is 15.2. However, the CUDA drivers on the A100s I have access to have been kept back to 12.2 for some reason.

With 5 different randomly generated positions, time taken to generate pairs for these positions is approximately 70ms. Using the CPU on the node of the GPU (I think it’s Intel Xeon Gold 5320), time to find the same pairs is around 2.27s - roughly 32.4x faster. My laptop CPU (AMD 8845hs) takes about 1.30s which means the GPU speedup is more like a 18.6x.

A fairly significant drawback of the algorithm here is that it consumes a lot of memory. On average, the potential pair list will consume 81/(4pi) ~ 6.5x more memory than the actual pair list. this is due to the search space being a cube of length 3r, and the actual “pair” space being a sphere of radius r. Indeed, for this test case, the potential pair list ends up being around 340e6 elements, and the actual pair list is about 55e6.

If we halve the cell size used in this algorithm, the search space decreases by a multiple of (5/6)^3 ~= 0.58. This is because the search region decreases from 6*cutoff to 5*cutoff. On the other hand, the grid size is increased by 8x. To test this change in the code, cells_per_cutoff = 1 can be changed to cells_per_cutoff = 2.

After this change, both the CPU and GPU times are improved. The GPU time goes down to approx. 38.5ms and the best CPU time on my laptop goes down to 1.08s, which means the GPU is about 28x faster after halving the cell size to be half the cutoff radius.

Times when using cell size of 1 cutoff distance:

Test No.	AMD 8845hs CPU (1 core)	Intel Xeon Gold 5320 (?) CPU (1 core)	NVIDIA A100 40GB PCIE
0	1,302,816	2,270,481	66,773
1	1,277,524	2,275,148	68,877
2	1,293,674	2,271,051	72,801
3	1,303,622	2,262,606	68,817
4	1,301,695	2,269,497	72,792

Times when using cell size of 2 cutoff distances:

Test No.	AMD 8845hs CPU (1 core)	Intel Xeon Gold 5320 (?) CPU (1 core)	NVIDIA A100 40GB PCIE
0	1,095,293	1,917,234	39,036
1	1,060,066	1,916,948	38,466
2	1,080,604	1,917,818	38,535
3	1,073,272	1,914,739	38,492
4	1,103,100	1,913,439	38,247

All times are in microseconds.

The number of potential pairs decreases from around 3.4e8 to 2.0e8, which is quite close to the estimated reduction. The number of grid cells goes up from 4.7e4 to 3.6e5, but the increase in grid size is far outweighed by the savings in number of potential pairs. Increasing cells_per_cutoff to 3 gives a segmentation fault - something to fix later…

Timings on more NVIDIA GPUs #

I have access to a couple other NVIDIA GPU models: the 4060 on my laptop, and the V100 SXM2 available on Australia’s national HPC. These are tested using the CUDA compatible with their driver versions (CUDA 13.0 for the laptop GPU and 12.9 for the V100).

cells_per_cutoff = 1 (times in microseconds):

Test No.	RTX 4060 Laptop	V100 SXM2
0	129,026	273,390
1	118,909	244,307
2	118,061	242,003
3	115,862	242,124
4	120,650	241,957

cells_per_cutoff = 2 (times in microseconds):

Test No.	RTX 4060 Laptop	V100 SXM2
0	97,391	68,541
1	80,113	52,337
2	79,696	52,359
3	80,592	51,514
4	80,473	54,169

The laptop GPU performance was quite good - achieving roughly half the performance at 14% of the TDP of the A100 (35W vs 250W). I was a bit worried about the V100 when cells_per_cutoff = 1, but its performance improved dramatically for cells_per_cutoff = 2.

Timings with AMD GPUs #

Getting the code to work with GPUs was fairly trivial. I only needed to make sure I had a working ROCm version with hipcc and rocthrust installed. These came with the rocm debian package. The compilation command used was

hipcc test.cu

Which compiles with O3 by default. The only code change I needed was to swap out cudaDeviceSynchronize with hipDeviceSynchronize and remove the NVTX code. ROCm used here are 6.4.1 for the MI250X tests and 6.4.4 for the 780m tests.

cells_per_cutoff = 1 (times in microseconds):

Test No.	AMD MI250X (1 GCD)	AMD 780m
0	147,227	515,262
1	134,363	498,018
2	134,714	501,888
3	133,510	507,251
4	134,214	543,599

cells_per_cutoff = 2 (times in microseconds):

Test No.	AMD MI250X (1 GCD)	AMD 780m
0	31,982	370,167
1	26,035	348,793
2	25,956	348,691
3	26,083	353,354
4	25,915	360,320

The MI250X impressed me with its performance at cells_per_cutoff = 2 - achieving the fastest times of all the GPUs tested here and achieving an approx 1080/26 ~= 41.5x speedup over the fastest CPU single-core time.

I wasn’t expecting good performance from my laptop’s integrated 780m graphics, but it was useful to see how portable the code really was.

Memory saving strategies? #

Conclusions #

Relative to single-core CPU code, the thrust code running on the GPU was seen to be between 28-40.5x faster - depending on the hardware used to do the comparison. For the condition where number of neighbours per point/particle are fixed, the time complexity is O(n). This scenario is representative of particle simulations like Discrete Element Method and Smoothed Particle Hydrodynamics where neighbours are kept fixed as more particles are introduced. A useful property of the algorithm shown here is that the order of pairs found is deterministic and reproducible, but with a significant memory overhead.

As a whole, I find thrust not too difficult to use, as a fairly unsophisticated C++ programmer. It abstracts a lot of the GPU programming, and gives access to very useful and optimised algorithms, while also being fairly platform portable. I only have two main gripes with it. The first is that making the low-level features unavailable makes it a little difficult to get the best performance for complex kernels, but I believe that to be intentional and part of the design. The second issue is the lack of examples. It feels like you have to be a fairly knowledgable programmer to parse the documentation - although ChatGPT makes it a lot easier.

I’m tempted to compare Thrust with Kokkos, which also aims to provide a performance portable programming framework. Kokkos is much more beginner friendly, with a long spiel about the programming model, good quality examples, and lots of public training material. It also gives gives access to low-level features such as shared memory and block through abstractions such as scratch space and teams. However, while most of their key algorithms perform really well, others like Kokkos::parallel_scan and Kokkos::sort resort to thrust under the hood (they had originally written their own versions of these algorithms, but they performed quite poorly).

Full code #

find_pairs.hpp #

#include <thrust/host_vector.h>                // thrust::host_vector
#include <thrust/device_vector.h>              // thrust::device_vector
#include <thrust/sort.h>                       // thrust::sort_by_key
#include <thrust/gather.h>                     // thrust::gather
#include <thrust/iterator/counting_iterator.h> // thrust::counting_iterator
#include <utility>                             // std::pair
#include <thrust/remove.h>                     // thrust::remove_if
#include <thrust/sequence.h>                    // thrust::sequence
#include <nvtx3/nvToolsExt.h>                  // nvtxRangePush, nvtxRangePop

// define constants
                // cell size is cutoff/cells_per_cutoff
constexpr int cells_per_cutoff = 2,
                // the length of the cube that forms the search space (units: no. of cells)
                search_cube_len = 2*cells_per_cutoff + 1,
                // no. of adjacent cells to search
                n_search_adj_cells = (search_cube_len*search_cube_len*search_cube_len - 1)/2,
                // no. of cells to search i.e. the number of adjacent cell plus the particle's own cell.
                n_search_all_cells = n_search_adj_cells + 1;

// thrust version
template<typename F>
std::pair<thrust::device_vector<int>, thrust::device_vector<int>> find_pairs_demo(
    thrust::device_vector<F> &x, 
    thrust::device_vector<F> &y, 
    thrust::device_vector<F> &z, 
    const F cutoff
) {

    nvtxRangePush("find_pairs");

    nvtxRangePush("setup");
    // define constant size of each cell
    const F cell_size = cutoff/F(cells_per_cutoff);

    const thrust::device_ptr<F> d_x {x.data()}, d_y {y.data()}, d_z {z.data()};

    nvtxRangePop();

    nvtxRangePush("grid");
    
    // find min-max extents
    F mingrid[3], maxgrid[3];
    auto res = thrust::minmax_element(x.begin(), x.end());
    mingrid[0] = *(res.first);
    maxgrid[0] = *(res.second);
    res = thrust::minmax_element(y.begin(), y.end());
    mingrid[1] = *(res.first);
    maxgrid[1] = *(res.second);
    res = thrust::minmax_element(z.begin(), z.end());
    mingrid[2] = *(res.first);
    maxgrid[2] = *(res.second);

    for (int d = 0; d < 3; ++d) {
        mingrid[d] -= F(2.)*cutoff;
        maxgrid[d] += F(2.)*cutoff;
    }

    const int ngrid[3] {
        static_cast<int>((maxgrid[0]-mingrid[0])/cell_size) + 1,
        static_cast<int>((maxgrid[1]-mingrid[1])/cell_size) + 1,
        static_cast<int>((maxgrid[2]-mingrid[2])/cell_size) + 1
    };

    nvtxRangePop();
    
    nvtxRangePush("map points to grid");

    // declare array to store particles' grid indices
    thrust::device_vector<int> gidx(x.size());
    // this makes the device vector's data accessible in the lambda
    const thrust::device_ptr<int> d_gidx {gidx.data()};

    // map particles to grid
    thrust::transform(
        thrust::make_zip_iterator(thrust::make_tuple(x.begin(), y.begin(), z.begin())),
        thrust::make_zip_iterator(thrust::make_tuple(x.end(), y.end(), z.end())),
        gidx.begin(),
        [=] __device__ (const thrust::detail::tuple_of_iterator_references<F&, F&, F&> in) {
            const int idxx = static_cast<int>((thrust::get<0>(in)-mingrid[0])/cell_size), // x grid index
                      idxy = static_cast<int>((thrust::get<1>(in)-mingrid[1])/cell_size), // y grid index
                      idxz = static_cast<int>((thrust::get<2>(in)-mingrid[2])/cell_size); // z grid index
            return idxy*ngrid[1]*ngrid[2] + idxx*ngrid[2] + idxz; // convert to 1D grid index and return
        }
    );
    
    nvtxRangePop();

    nvtxRangePush("sort particles");

    // sort particles based on grid index. Performed in a block to manage scratch space.
    {
        // initialize permute
        thrust::device_vector<int> permute(x.size());
        thrust::sequence(permute.begin(), permute.end()); // e.g., 0 1 2 3 4

        // sort gidx
        thrust::sort_by_key(thrust::device, gidx.begin(), gidx.end(), permute.begin());
        /* e.g. before gidx = 1 9 2 8 3, permute = 0 1 2 3 4
                after  gidx = 1 2 3 8 9, permute = 0 2 4 3 1 */

        // gather old positions into new ones
        thrust::device_vector<F> tmp(x.size());
        thrust::gather(thrust::device, permute.begin(), permute.end(), x.begin(), tmp.begin());
        /* e.g. before x = 0.1 0.5 0.1 0.5 0.3, tmp = ?   ?   ?   ?   ?
                after  x = "                 ", tmp = 0.1 0.1 0.3 0.5 0.5 */
        thrust::copy(thrust::device, tmp.begin(), tmp.end(), x.begin());
        // e.g.        x = 0.1 0.1 0.3 0.5 0.5
        // repeat for y, z
        thrust::gather(thrust::device, permute.begin(), permute.end(), y.begin(), tmp.begin());
        thrust::copy(thrust::device, tmp.begin(), tmp.end(), y.begin());
        thrust::gather(thrust::device, permute.begin(), permute.end(), z.begin(), tmp.begin());
        thrust::copy(thrust::device, tmp.begin(), tmp.end(), z.begin());
    }

    nvtxRangePop();
    
    nvtxRangePush("find cell ends");

    // initialize cell_ends vector and initialize to 0
    thrust::device_vector<int> cell_ends(ngrid[0]*ngrid[1]*ngrid[2], 0);
    // create device_ptr needed for lambda
    thrust::device_ptr<int> d_cell_ends {cell_ends.data()};
    thrust::for_each(
        thrust::counting_iterator<int>(1), 
        thrust::counting_iterator<int>(gidx.size()), 
        [=] __device__ (const int i) {
            const int this_cell = d_gidx[i], prev_cell = d_gidx[i-1];
            if (this_cell != prev_cell) d_cell_ends[prev_cell] = i;
        }
    );
    // e.g. gidx = 1 2 3 8 9, cell_ends = 0 1 2 3 0 0 0 0 0 4 5 0
    thrust::inclusive_scan(thrust::device, cell_ends.begin(), cell_ends.end(), cell_ends.begin(), thrust::maximum<int>());
    // e.g. cell_ends = 0 1 2 3 3 3 3 3 3 4 5 5

    nvtxRangePop();
    
    nvtxRangePush("populate nchecks");

    // initialize number of checks
    thrust::device_vector<size_t> nchecks(n_search_all_cells*x.size());
    thrust::device_ptr<size_t> d_nchecks {nchecks.data()};

    // populate nchecks
    thrust::for_each(
        thrust::counting_iterator<int>(0),
        thrust::counting_iterator<int>(x.size()),
        [=] __device__ (const int i) {
            const int loc = n_search_all_cells*i, my_idx = d_gidx[i];
            int start_idx = my_idx - cells_per_cutoff*ngrid[2]*ngrid[1] - cells_per_cutoff*ngrid[2] - cells_per_cutoff;
            for (int j = 0; j < n_search_all_cells; ++j) {
                // which cell am i comparing to?
                const int idxz = j % search_cube_len,
                          rem = j / search_cube_len, 
                          idxy = rem % search_cube_len, 
                          idxx = rem / search_cube_len;
                const int neighbour_idx = start_idx + idxx*ngrid[1]*ngrid[2] + idxy*ngrid[2] + idxz;
                // get the starting particle index
                const int start_pidx = d_cell_ends[neighbour_idx-1];
                const int end_pidx = j==n_search_adj_cells ? i : d_cell_ends[neighbour_idx];
                d_nchecks[loc+j] = static_cast<size_t>(end_pidx - start_pidx);
            }
        }
    );

    const size_t last_ncheck_prescan = nchecks.back();
    thrust::exclusive_scan(thrust::device, nchecks.begin(), nchecks.end(), nchecks.begin());
    const size_t nchecks_total = last_ncheck_prescan + nchecks.back();

    nvtxRangePop();
    
    nvtxRangePush("generate potential pairs");

    // initialize potential pair list
    thrust::device_vector<int> potential_pairs_i(nchecks_total), potential_pairs_j(nchecks_total);
    thrust::device_ptr<int> d_potential_pairs_i(potential_pairs_i.data()), d_potential_pairs_j(potential_pairs_j.data());

    // allocate vector to flag which potential pair is an actual pair
    thrust::device_vector<bool> is_neighbour(nchecks_total);
    const thrust::device_ptr<bool> d_is_neighbour {is_neighbour.data()};

    // search potential pairs and flag actual pairs
    thrust::for_each(
        thrust::counting_iterator<int>(0),
        thrust::counting_iterator<int>(nchecks.size()),
        [=] __device__ (const int ii) {
            const int i = ii/n_search_all_cells, neighbour = ii % n_search_all_cells;
            const int my_idx = d_gidx[i], 
                      start_idxz = neighbour % search_cube_len, 
                      rem = neighbour/search_cube_len, 
                      start_idxx = rem / search_cube_len, 
                      start_idxy = rem % search_cube_len;
            const int neighbour_idx = 
                      my_idx + 
                      ngrid[1]*ngrid[2]*(start_idxx-cells_per_cutoff) + 
                      ngrid[2]*(start_idxy-cells_per_cutoff) + 
                      (start_idxz - cells_per_cutoff);
            const int start_idx = d_cell_ends[neighbour_idx - 1], 
                      end_idx = neighbour==n_search_adj_cells ? i : d_cell_ends[neighbour_idx];
            size_t loc = d_nchecks[ii];
            const F xi = d_x[i], yi = d_y[i], zi = d_z[i];
            for (int j = start_idx; j < end_idx; ++j) {
                const F dx = xi - d_x[j], dy = yi - d_y[j], dz = zi - d_z[j];
                d_is_neighbour[loc] = (dx*dx + dy*dy + dz*dz < cutoff*cutoff);
                // faster to always save pairs - even if not an actual pair.
                d_potential_pairs_i[loc] = i;
                d_potential_pairs_j[loc] = j;
                loc++;
            }
        }
    );

    nvtxRangePop();

    nvtxRangePush("compact potential pairs");

    potential_pairs_i.erase(
        thrust::remove_if(
            potential_pairs_i.begin(), 
            potential_pairs_i.end(), 
            is_neighbour.begin(), 
            thrust::logical_not<bool>()
        ),
	    potential_pairs_i.end()
    );
    potential_pairs_j.erase(
        thrust::remove_if(
            potential_pairs_j.begin(), 
            potential_pairs_j.end(), 
            is_neighbour.begin(), 
            thrust::logical_not<bool>()
        ),
	    potential_pairs_j.end()
    );

    nvtxRangePop();

    // return indices as a pair of vectors
    std::pair<thrust::device_vector<int>, thrust::device_vector<int>> 
        pairs_out(
            std::move(potential_pairs_i), 
            std::move(potential_pairs_j)
        );

    // end of the range started at the start of the function
    nvtxRangePop();

    return pairs_out;
}

// cpu version
template<typename F>
std::pair<std::vector<int>, std::vector<int>> find_pairs(std::vector<F> &x, std::vector<F> &y, std::vector<F> &z, F cutoff) {

    const F cell_size = cutoff/F(cells_per_cutoff);

    // get grid dims
    F mingrid[3] {x[0], y[0], z[0]}, maxgrid[3] {x[0], y[0], z[0]};
    for (int i = 1; i < x.size(); ++i) {
        mingrid[0] = x[i] < mingrid[0] ? x[i] : mingrid[0];
        mingrid[1] = y[i] < mingrid[1] ? y[i] : mingrid[1];
        mingrid[2] = z[i] < mingrid[2] ? z[i] : mingrid[2];
        maxgrid[0] = x[i] > maxgrid[0] ? x[i] : maxgrid[0];
        maxgrid[1] = y[i] > maxgrid[1] ? y[i] : maxgrid[1];
        maxgrid[2] = z[i] > maxgrid[2] ? z[i] : maxgrid[2];
    }
    for (int d = 0; d < 3; ++d) {
        mingrid[d] -= F(2.)*cell_size;
        maxgrid[d] += F(2.)*cell_size;
        
    }
    const int ngrid[3] {
        static_cast<int>((maxgrid[0]-mingrid[0])/cell_size) + 1,
        static_cast<int>((maxgrid[1]-mingrid[1])/cell_size) + 1,
        static_cast<int>((maxgrid[2]-mingrid[2])/cell_size) + 1
    };
    for (int d = 0; d < 3; ++d) maxgrid[d] = mingrid[d] + (ngrid[d]-1)*cell_size;

    // assign particles to grid
    std::vector<int> gidx(x.size());
    for (int i = 0; i < gidx.size(); ++i) {
        gidx[i] = static_cast<int>((x[i]-mingrid[0])/cell_size)*ngrid[1]*ngrid[2] +
                  static_cast<int>((y[i]-mingrid[1])/cell_size)*ngrid[2] +
                  static_cast<int>((z[i]-mingrid[2])/cell_size);
    }

    // sorting particles
    std::vector<int> permute(gidx.size());
    for (int i = 0; i < gidx.size(); ++i) permute[i] = i;

    std::sort(
        permute.begin(),
        permute.end(),
        [&](const int& a, const int& b) {
            return gidx[a] < gidx[b];
        }
    );

    std::vector<int> gidx_tmp(gidx.size());
    std::vector<F> xtmp(x.size()), ytmp(y.size()), ztmp(z.size());
    for (int i = 0; i < permute.size(); ++i) {
        gidx_tmp[i] = gidx[permute[i]];
        xtmp[i] = x[permute[i]];
        ytmp[i] = y[permute[i]];
        ztmp[i] = z[permute[i]];
    }
    for (int i = 0; i < permute.size(); ++i) {
        gidx[i] = gidx_tmp[i];
        x[i] = xtmp[i];
        y[i] = ytmp[i];
        z[i] = ztmp[i];
    }

    // find mapping
    std::vector<size_t> cell_ends(ngrid[0]*ngrid[1]*ngrid[2]);
    for (int i = 0; i < cell_ends.size(); ++i) cell_ends[i] = 0;
    for (int i = 1; i < gidx.size(); ++i) {
        int prev_cell = gidx[i-1];
        int this_cell = gidx[i];
        if (prev_cell != this_cell) cell_ends[prev_cell] = i;
    }
    size_t maxval = 0;
    for (int i = 0; i < cell_ends.size(); ++i) {
        maxval = cell_ends[i] > maxval ? cell_ends[i] : maxval;
        cell_ends[i] = maxval;
    }

    std::pair<std::vector<int>, std::vector<int>> pairs;
    int npairs = 0;
    for (int i = 0; i < x.size(); ++i) {
        const int my_idx = gidx[i];
        const F xi = x[i], yi = y[i], zi = z[i];
        for (int didx_x = -cells_per_cutoff; didx_x < 0; ++didx_x) {
            for (int didx_y = -cells_per_cutoff; didx_y <= cells_per_cutoff; ++didx_y) {
                const int startidx = my_idx + didx_x*ngrid[1]*ngrid[2] + didx_y*ngrid[2] - cells_per_cutoff;
                for (int j = cell_ends[startidx-1]; j < cell_ends[startidx+search_cube_len-1]; ++j) {
                    const F dx = xi - x[j], dy = yi - y[j], dz = zi - z[j];
                    if (dx*dx+dy*dy+dz*dz < cutoff*cutoff) {
                        pairs.first.push_back(i);
                        pairs.second.push_back(j);
                        npairs++;
                    }
                }
            }
        }
        for (int didx_y = -cells_per_cutoff; didx_y < 0; ++didx_y) {
            const int startidx = my_idx + didx_y*ngrid[2] - cells_per_cutoff;
            for (int j = cell_ends[startidx-1]; j < cell_ends[startidx+search_cube_len-1]; ++j) {
                const F dx = xi - x[j], dy = yi - y[j], dz = zi - z[j];
                if (dx*dx+dy*dy+dz*dz < cutoff*cutoff) {
                    pairs.first.push_back(i);
                    pairs.second.push_back(j);
                    npairs++;
                }
            }
        }
        for (int j = cell_ends[my_idx-cells_per_cutoff-1]; j < i; ++j) {
            const F dx = xi - x[j], dy = yi - y[j], dz = zi - z[j];
            if (dx*dx+dy*dy+dz*dz < cutoff*cutoff) {
                pairs.first.push_back(i);
                pairs.second.push_back(j);
                npairs++;
            }
        }
    }

    return pairs;

}

demo.cpp #

#include <find_pairs.hpp>
#include <iostream>
#include <chrono>
#include <random>


int main(int argc, char* argv[]) {
    const size_t nx = 100, ny = 100, nz = 100, ntotal = nx*ny*nz;
    const double dx = 1./nx, cutoff = 3.*dx;
    thrust::host_vector<double> h_x(ntotal), h_y(ntotal), h_z(ntotal);
    std::uniform_real_distribution<double> unif(0., 1.);
    std::default_random_engine re;
    for (int i = 0; i < 5; ++i) {

        std::cout << "test" << i << '\n';

        for (int i = 0; i < ntotal; ++i) {
            h_x[i] = unif(re);
            h_y[i] = unif(re);
            h_z[i] = unif(re);
        }

        // for validation
        thrust::device_vector<double> d_x {h_x}, d_y {h_y}, d_z {h_z};

        // wait for copy to device to finish
        cudaDeviceSynchronize();

        auto start = std::chrono::high_resolution_clock::now();
        std::pair<thrust::device_vector<int>, thrust::device_vector<int>> pairs_gpu = find_pairs_demo(d_x, d_y, d_z, cutoff);
        cudaDeviceSynchronize();
        auto stop = std::chrono::high_resolution_clock::now();
        auto duration = std::chrono::duration_cast<std::chrono::microseconds>(stop-start);
        std::cout << "  GPU thrust:\n";
        std::cout << "    Time taken by function: " << duration.count() << " us\n";
        std::cout << "    Number of pairs: " << pairs_gpu.first.size() << '\n';

        // validate
        std::vector<double> vx(h_x.size()), vy(h_y.size()), vz(h_z.size());
        for (size_t i = 0; i < h_x.size(); ++i) {
            vx[i] = h_x[i];
            vy[i] = h_y[i];
            vz[i] = h_z[i];
        }
        std::vector<int> pair_i(100*ntotal), pair_j(100*ntotal);
        start = std::chrono::high_resolution_clock::now();
        std::pair<std::vector<int>, std::vector<int>> pairs_cpu = find_pairs(vx, vy, vz, cutoff);
        stop = std::chrono::high_resolution_clock::now();
        duration = std::chrono::duration_cast<std::chrono::microseconds>(stop-start);

        std::cout << "  CPU:\n";
        std::cout << "    Time taken by function: " << duration.count() << " us\n";
        std::cout << "    Number of pairs: " << pairs_cpu.first.size() << '\n';

    }

}