Cell-lists point-pairs search with fixed cutoff - reducing search space #
Description #
The naive cell-list pair search, is a good
start. But a drawback of that implementation is that it searches through all adjacent cells, and uses an if
statement to avoid duplicate checks. However, looping over all adjacent cells still takes time, and the if
statement can be expensive by introducing branching.
However, to eliminate duplicate checks, we only need to compare particles in the current cell with particles in half of the adjacent cells. For instance, if you’ve checked particle A in one cell against particle B in a neighboring cell, you don’t need to check B against A again when you move to that neighboring cell. Hence, you can omit some cells from the search for each particle to avoid this redundancy. See below sketches that illustrate how coverage is not reduced with this strategy.
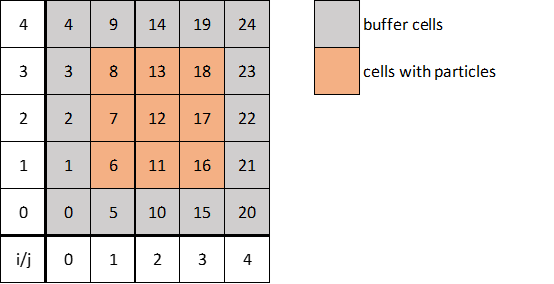
Sketch showing a 2D grid that would be used to perform the pair search. The grid is setup to include at least one buffer layer of cells
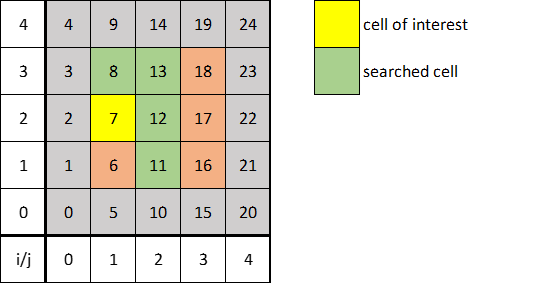
When looping over each particle to find pairs, the particles’ cell will be searched, as well as 4 adjacent cells. This reduces the search space from 9 cells, to 5 cells in 2D; and 27 cells, to 14 cells in 3D.
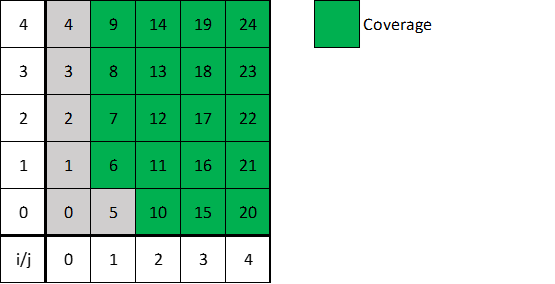
The coverage still contains the cells with particles, and the only cells missed are empty buffer cells.
The code below copies the setup code from the naive implementation, but makes modifications to reduce the
search space. Note the introduction of the idxs parameter array used to selectively loop through adjacent
cells.
Additional notes #
I observed about 1.5x speedup on finding pairs in 100,000 elements, with default optimisation, but this speedup
vanishes if compiling with -O1 and above.
Subsequent pages will demonstrate how this algorithmic optimisation can still be useful.
Code (Fortran) #
Save the code as cll2.F90, and compile it with:
gfortran -o cll2.x cll2.F90
! Module to perform direct search for pairs of points within a fixed cutoff.
! cellList subroutine
! dim: An integer defining dimension of the coordinates.
! npoints: An integer with number of points.
! maxpercell: An integer with max number of points in a cell.
! x: An real/real(f) array of dim x points dimension containing the list of points to find pairs of.
! cutoff: The distance (same type as x) which defines a pair
! maxnpair: An integer of the maximum number of pairs expected.
! npairs: An integer with the number of pairs found.
! pair_i: An integer array of maxnpairs length with the "left-sided" point in a pair.
! pair_j: An integer array of maxnpairs length with the "right-sided" point in a pair.
module cellList_m
use iso_fortran_env, only: error_unit
public
private:: coordsToCell
#ifdef SINGLEPRECISION
parameter, integer:: f = kind(1.)
#else
parameter, integer:: f = kind(1.d0)
#endif
contains
!---------------------------------------------------------------------------
function coordsToCell(dim, xi, minx, cutoff) result(icell)
implicit none
real(f), intent(in):: xi(dim), minx(3), cutoff
integer, intent(in):: dim
integer:: icell(3)
icell(1:dim) = int((xi(:) - minx(1:dim))/cutoff) + 1
if (dim == 2) icell(3) = 1
end function coordsToCell
!---------------------------------------------------------------------------
subroutine cellList(dim, npoints, maxpercell, x, cutoff, maxnpair, npairs, pair_i, pair_j)
implicit none
integer, intent(in):: dim, npoints, maxnpair, maxpercell
real(f), intent(in):: x(dim, npoints), cutoff
integer, intent(out):: npairs, pair_i(maxnpair), pair_j(maxnpair)
integer:: i, j, k, kk, ngridx(3), icell(3), xi, yi, zi, jcell(3)
real(f):: r2, minx(3), maxx(3)
integer, allocatable:: pincell(:, :, :), cells(:, :, :, :)
! Below array is used to store which adjacent cells to search through
integer, parameter:: sweep_idxs(3, 13) = reshape([-1, -1, -1, &
-1, -1, 0, &
-1, -1, 1, &
-1, 0, -1, &
-1, 0, 0, &
-1, 0, 1, &
-1, 1, -1, &
-1, 1, 0, &
-1, 1, 1, &
0, -1, -1, &
0, -1, 0, &
0, -1, 1, &
0, 0, -1], [3, 13])
! determine grid min-max coordinates, with concessions made for dim=2 case
minx(1:dim) = minval(x, dim=2)
if (dim == 2) minx(3) = 0.d0
maxx(1:dim) = maxval(x, dim=2)
if (dim == 2) maxx(3) = 0.d0
! creating buffer layers
minx(:) = minx(:) - 2.d0*cutoff
maxx(:) = maxx(:) + 2.d0*cutoff
! initializing grid arrays
allocate (pincell(ngridx(1), ngridx(2), ngridx(3)), &
cells(maxpercell, ngridx(1), ngridx(2), ngridx(3)))
pincell(:, :, :) = 0
! populating grid with point information
do i = 1, npoints
icell = coordsToCell(dim, x(:, i), minx, cutoff)
pincell(icell(1), icell(2), icell(3)) = &
pincell(icell(1), icell(2), icell(3)) + 1
#ifdef DEBUG
if (pincell(icell(1), icell(2), icell(3)) > maxpercell) then
write (error_unit, '(A, 3(I2, 1x), A)') 'Number of particles in cell ', icell(1), icell(2), icell(3), &
' exceeds the input maxpercell value.'
write (error_unit, '(A)') 'Terminating...'
error stop 1
end if
#endif
cells(pincell(icell(1), icell(2), icell(3)), icell(1), icell(2), icell(3)) = i
end do
npairs = 0
do i = 1, npoints
icell(:) = coordsToCell(dim, x(:, i), minx, cutoff)
! first loop to search through particle i's cell
do k = 1, pincell(icell(1), icell(2), icell(3))
j = cells(k, icell(1), icell(2), icell(3))
if (j > i) then
r2 = sum((x(:, i) - x(:, j))**2)
if (r2 <= cutoff**2) then
npairs = npairs + 1
pair_i(npairs) = i
pair_j(npairs) = j
end if
end if
end do
! second loop to search through adjacent 13 cells
do kk = 1, 13
jcell(:) = icell(:) + sweep_idxs(:, kk)
do k = 1, pincell(jcell(1), jcell(2), jcell(3))
j = cells(k, jcell(1), jcell(2), jcell(3))
r2 = sum((x(:, i) - x(:, j))**2)
if (r2 <= cutoff**2) then
npairs = npairs + 1
pair_i(npairs) = i
pair_j(npairs) = j
end if
end do
end do
end do
end subroutine cellList
end module cellList_m
#ifndef NOMAIN
program main
use cellList_m, only: f, cellList
implicit none
integer, parameter:: n = 100, dim = 3, maxnpair = 60*n ! estimated using
! 2x the coaxial spacing if the points were arranged in a square
real(f), parameter:: cutoff = 2*n**(-1.d0/dim)
integer:: npairs, k
real(f), allocatable:: x(:, :)
integer, allocatable:: pair_i(:), pair_j(:)
allocate(x(dim, n), pair_i(maxnpair), pair_j(maxnpair))
! initialize positions with pseudo-random numbers
call random_number(x)
! finding pairs
call cellList(dim, n, 27, x, cutoff, maxnpair, npairs, pair_i, pair_j)
write (*, '(A)') 'Executing cellList'
write (*, '(2x, A,I4,A)') 'Found ', npairs, ' pairs'
write (*, '(2x, A)') 'First and last 5 pairs of points found:'
write (*, '(2x, 4(A4, 1x))') 'Pair', 'i', 'j'
do k = 1, npairs
if (k <= 5 .or. k > npairs - 4) write (*, '(2x, 3(I4, 1x))') k, &
pair_i(k), pair_j(k)
if (k == 6) write (*, '(2x, A)') '...'
end do
end program main
#endif